We’ve all seen the formula for the sum of the first n integers:

A similar formula exists for the sum of the squares of the first n integers.
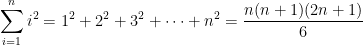
One day during a particularly boring lecture in one of my gen-ed undergraduate courses I was playing with these formulas and I stumbled across a recursive formula for the sum of the first n integers taken to any integer power. That is,
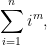 where
where 
Let’s define a function S such that 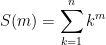 . The domain of S is the set of nonnegative integers. Let’s begin by investigating several small values of m.
. The domain of S is the set of nonnegative integers. Let’s begin by investigating several small values of m.
 To derive an iterative formula for
To derive an iterative formula for 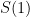 , let’s investigate the function
, let’s investigate the function  . Let’s partition the interval
. Let’s partition the interval ![[0, n]](https://s0.wp.com/latex.php?latex=%5B0%2C+n%5D&bg=ffffff&fg=000000&s=0&c=20201002) into unit subintervals:
into unit subintervals: ![I_k = [k-1, k], k=1, 2, \dots, n](https://s0.wp.com/latex.php?latex=I_k+%3D+%5Bk-1%2C+k%5D%2C+k%3D1%2C+2%2C+%5Cdots%2C+n&bg=ffffff&fg=000000&s=0&c=20201002) , and draw a rectangle in each subinterval with bottom-left corner at
, and draw a rectangle in each subinterval with bottom-left corner at ![[k-1, 0]](https://s0.wp.com/latex.php?latex=%5Bk-1%2C+0%5D&bg=ffffff&fg=000000&s=0&c=20201002) and top-right corner at
and top-right corner at ![[k, k]](https://s0.wp.com/latex.php?latex=%5Bk%2C+k%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
This is similar to using a right endpoint approximation of the definite integral using rectangles. Since each rectangle has a base of 1 and height of k, then the sum of the areas of these rectangles is  .
.
Let’s find the sum of the areas of the rectangles by partitioning each rectangle into two parts: the parts above (pink) and below the curve (red). Adding them together will give the area of any particular rectangle.
![\begin{array}{rcl} S(1) & = & \displaystyle\int_{0}^{n}xdx + \sum_{k=1}^{n}\left[\int_{k-1}^{k}(k-x)dx\right] \\ & = & \displaystyle\frac{n^2}{2}+\sum_{k=1}^n \left[ \left. \left( kx-\frac{x^2}{2} \right) \right|_{k-1}^k \right] \\ & = & \displaystyle\frac{n^2}{2}+\sum_{k=1}^n \left[k (k - (k - 1))-\left(\frac{k^2}{2} - \frac{(k-1)^2}{2}\right) \right] \\ & = & \displaystyle\frac{n^2}{2}+\sum_{k=1}^n \left[k -\left(\frac{k^2}{2} - \frac{k^2-2k+1}{2}\right) \right] \\ & = & \displaystyle\frac{n^2}{2}+\sum_{k=1}^n \left[\frac{2k - k^2 + k^2 - 2k + 1}{2} \right] \\ & = & \displaystyle\frac{n^2}{2}+\sum_{k=1}^n \frac{1}{2} \\ & = & \displaystyle\frac{n^2}{2} + \frac{1}{2}S(0) \\ & = & \displaystyle\frac{n^2}{2} + \frac{n}{2} \\ & = & \displaystyle\frac{n(n+1)}{2} \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++S%281%29+%26+%3D+%26+%5Cdisplaystyle%5Cint_%7B0%7D%5E%7Bn%7Dxdx+%2B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5B%5Cint_%7Bk-1%7D%5E%7Bk%7D%28k-x%29dx%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D%2B%5Csum_%7Bk%3D1%7D%5En+%5Cleft%5B+%5Cleft.+%5Cleft%28+kx-%5Cfrac%7Bx%5E2%7D%7B2%7D+%5Cright%29+%5Cright%7C_%7Bk-1%7D%5Ek+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D%2B%5Csum_%7Bk%3D1%7D%5En+%5Cleft%5Bk+%28k+-+%28k+-+1%29%29-%5Cleft%28%5Cfrac%7Bk%5E2%7D%7B2%7D+-+%5Cfrac%7B%28k-1%29%5E2%7D%7B2%7D%5Cright%29+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D%2B%5Csum_%7Bk%3D1%7D%5En+%5Cleft%5Bk+-%5Cleft%28%5Cfrac%7Bk%5E2%7D%7B2%7D+-+%5Cfrac%7Bk%5E2-2k%2B1%7D%7B2%7D%5Cright%29+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D%2B%5Csum_%7Bk%3D1%7D%5En+%5Cleft%5B%5Cfrac%7B2k+-+k%5E2+%2B+k%5E2+-+2k+%2B+1%7D%7B2%7D+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D%2B%5Csum_%7Bk%3D1%7D%5En+%5Cfrac%7B1%7D%7B2%7D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D+%2B+%5Cfrac%7B1%7D%7B2%7DS%280%29+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%7D%7B2%7D+%2B+%5Cfrac%7Bn%7D%7B2%7D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%28n%2B1%29%7D%7B2%7D++%5Cend%7Barray%7D++&bg=ffffff&fg=000000&s=0&c=20201002)
Similarly, we can derive an iterative formula for  .
.
![\begin{array}{rcl} S(2) & = & \displaystyle\int_{0}^{n}x^2dx + \sum_{k=1}^{n}\left[\int_{k-1}^{k}(k^2-x^2)dx \right] \\ & = & \displaystyle\frac{n^3}{3} + \sum_{k=1}^{n}\left[k^2-\frac{k^3}{3} + \frac{(k-1)^3}{3} \right] \\ & = & \displaystyle\frac{n^3}{3} + \sum_{k=1}^{n}\left[ \frac{3k-1}{3} \right] \\ & = & \displaystyle\frac{n^3}{3} + S(1) - \frac{1}{3}S(0) \\ & = & \displaystyle\frac{n^3}{3} + \frac{n(n+1)}{2} - \frac{n}{3} \\ & = & \displaystyle\frac{n(n+1)(2n+1)}{6} \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++S%282%29+%26+%3D+%26+%5Cdisplaystyle%5Cint_%7B0%7D%5E%7Bn%7Dx%5E2dx+%2B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5B%5Cint_%7Bk-1%7D%5E%7Bk%7D%28k%5E2-x%5E2%29dx+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E3%7D%7B3%7D+%2B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5Bk%5E2-%5Cfrac%7Bk%5E3%7D%7B3%7D+%2B+%5Cfrac%7B%28k-1%29%5E3%7D%7B3%7D+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E3%7D%7B3%7D+%2B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5B+%5Cfrac%7B3k-1%7D%7B3%7D+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E3%7D%7B3%7D+%2B+S%281%29+-+%5Cfrac%7B1%7D%7B3%7DS%280%29+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E3%7D%7B3%7D+%2B+%5Cfrac%7Bn%28n%2B1%29%7D%7B2%7D+-+%5Cfrac%7Bn%7D%7B3%7D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%28n%2B1%29%282n%2B1%29%7D%7B6%7D++%5Cend%7Barray%7D++&bg=ffffff&fg=000000&s=0&c=20201002)
Let’s begin to investigate the general case 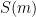 .
.
![\begin{array}{rcl} S(m) & = & \displaystyle\int_{0}^{n}x^mdx + \sum_{k=1}^{n}\left[\int_{k-1}^{k}(k^m-x^m)dx \right] \\ & = & \displaystyle\frac{n^{m+1}}{m+1} + \sum_{k=1}^{n}\left[k^m - \frac{k^{m+1}}{m+1} + \frac{(k-1)^{m+1}}{m+1} \right] \\ & = & \displaystyle\frac{n^{m+1}}{m+1} + \frac{1}{m+1}\left[ \sum_{k=1}^{n}\left[ (m+1)k^m - k^{m+1} + (k-1)^{m+1} \right] \right] \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++S%28m%29+%26+%3D+%26+%5Cdisplaystyle%5Cint_%7B0%7D%5E%7Bn%7Dx%5Emdx+%2B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5B%5Cint_%7Bk-1%7D%5E%7Bk%7D%28k%5Em-x%5Em%29dx+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%2B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5Bk%5Em+-+%5Cfrac%7Bk%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%2B+%5Cfrac%7B%28k-1%29%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%2B+%5Cfrac%7B1%7D%7Bm%2B1%7D%5Cleft%5B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5B+%28m%2B1%29k%5Em+-+k%5E%7Bm%2B1%7D+%2B+%28k-1%29%5E%7Bm%2B1%7D+%5Cright%5D+%5Cright%5D++%5Cend%7Barray%7D++&bg=ffffff&fg=000000&s=0&c=20201002)
But we can expand  using the Binomial Theorem.
using the Binomial Theorem.

Substituting into the above equation for 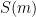 ,
,
![\displaystyle S(m) = \frac{n^{m+1}}{m+1} + \frac{1}{m+1}\left[ \sum_{k=1}^{n}\left[ (m+1)k^m - k^{m+1} + (k^{m+1} - (m+1)k^m + \cdots) \right] \right]](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+S%28m%29+%3D+%5Cfrac%7Bn%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%2B+%5Cfrac%7B1%7D%7Bm%2B1%7D%5Cleft%5B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%5Cleft%5B+%28m%2B1%29k%5Em+-+k%5E%7Bm%2B1%7D+%2B+%28k%5E%7Bm%2B1%7D+-+%28m%2B1%29k%5Em+%2B+%5Ccdots%29+%5Cright%5D+%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)
These terms cancel and filling in the 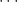 ,
,
![\begin{array}{rcl} S(m) & = & \displaystyle\frac{n^{m+1}}{m+1} + \frac{1}{m+1}\left[ \sum_{k=1}^{n} \left[ \binom{m+1}{2}k^{m-1} -+ \cdots + (-1)^{m}(m+1)k + (-1)^{m+1} \right] \right] \\ & = & \displaystyle\frac{n^{m+1}}{m+1} + \frac{1}{m+1}\left[ \sum_{i=2}^{m+1}(-1)^i\binom{m+1}{i}S(m+1-i)\right], \textrm{where } S(0) = n. \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++S%28m%29+%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%2B+%5Cfrac%7B1%7D%7Bm%2B1%7D%5Cleft%5B+%5Csum_%7Bk%3D1%7D%5E%7Bn%7D+%5Cleft%5B+%5Cbinom%7Bm%2B1%7D%7B2%7Dk%5E%7Bm-1%7D+-%2B+%5Ccdots+%2B+%28-1%29%5E%7Bm%7D%28m%2B1%29k+%2B+%28-1%29%5E%7Bm%2B1%7D+%5Cright%5D+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E%7Bm%2B1%7D%7D%7Bm%2B1%7D+%2B+%5Cfrac%7B1%7D%7Bm%2B1%7D%5Cleft%5B+%5Csum_%7Bi%3D2%7D%5E%7Bm%2B1%7D%28-1%29%5Ei%5Cbinom%7Bm%2B1%7D%7Bi%7DS%28m%2B1-i%29%5Cright%5D%2C+%5Ctextrm%7Bwhere+%7D+S%280%29+%3D+n.++%5Cend%7Barray%7D++&bg=ffffff&fg=000000&s=0&c=20201002)
Or if we write it in terms of  ,
,
![S(m - 1) = \displaystyle\frac{n^{m}}{m} + \frac{1}{m}\left[ \sum_{i=2}^{m}(-1)^i\binom{m}{i}S(m-i)\right], \textrm{where } S(0) = n](https://s0.wp.com/latex.php?latex=S%28m+-+1%29+%3D+%5Cdisplaystyle%5Cfrac%7Bn%5E%7Bm%7D%7D%7Bm%7D+%2B+%5Cfrac%7B1%7D%7Bm%7D%5Cleft%5B+%5Csum_%7Bi%3D2%7D%5E%7Bm%7D%28-1%29%5Ei%5Cbinom%7Bm%7D%7Bi%7DS%28m-i%29%5Cright%5D%2C+%5Ctextrm%7Bwhere+%7D+S%280%29+%3D+n&bg=ffffff&fg=000000&s=0&c=20201002) .
.
We now have a recursive formula for 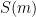 . Let’s try it out with
. Let’s try it out with 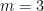
![\begin{array}{rcl} S(3) & = & \displaystyle\frac{n^4}{4} + \frac{1}{4} \left[ \binom{4}{2}S(2) - \binom{4}{3}S(1) + \binom{4}{4}S(0) \right] \\ & = & \displaystyle\frac{n^4}{4} + \frac{1}{4} \left[ 6\left( \frac{n(n+1)(2n+1)}{6} \right) - 4\left( \frac{n(n+1)}{2} \right) + n \right] \\ & = & \displaystyle\frac{1}{4} \left( n^4 + 2n^3 + 3n^2 + n - 2n^2 -2n + n \right) \\ & = & \displaystyle\frac{1}{4} ( n^4 + 2n^3 + n^2 ) \\ & = & \displaystyle\frac{n^2(n+1)^2}{4} \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Brcl%7D++S%283%29+%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E4%7D%7B4%7D+%2B+%5Cfrac%7B1%7D%7B4%7D+%5Cleft%5B+%5Cbinom%7B4%7D%7B2%7DS%282%29+-+%5Cbinom%7B4%7D%7B3%7DS%281%29+%2B+%5Cbinom%7B4%7D%7B4%7DS%280%29+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E4%7D%7B4%7D+%2B+%5Cfrac%7B1%7D%7B4%7D+%5Cleft%5B+6%5Cleft%28+%5Cfrac%7Bn%28n%2B1%29%282n%2B1%29%7D%7B6%7D+%5Cright%29+-+4%5Cleft%28+%5Cfrac%7Bn%28n%2B1%29%7D%7B2%7D+%5Cright%29+%2B+n+%5Cright%5D+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7B1%7D%7B4%7D+%5Cleft%28+n%5E4+%2B+2n%5E3+%2B+3n%5E2+%2B+n+-+2n%5E2+-2n+%2B+n+%5Cright%29+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7B1%7D%7B4%7D+%28+n%5E4+%2B+2n%5E3+%2B+n%5E2+%29+%5C%5C+++++++%26+%3D+%26+%5Cdisplaystyle%5Cfrac%7Bn%5E2%28n%2B1%29%5E2%7D%7B4%7D++%5Cend%7Barray%7D++&bg=ffffff&fg=000000&s=0&c=20201002)
The results for larger values of m are summarized in the following table.
The following table simply contains the coefficients of the expanded function  where the i-th entry is the coefficient of
where the i-th entry is the coefficient of 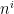 .
.
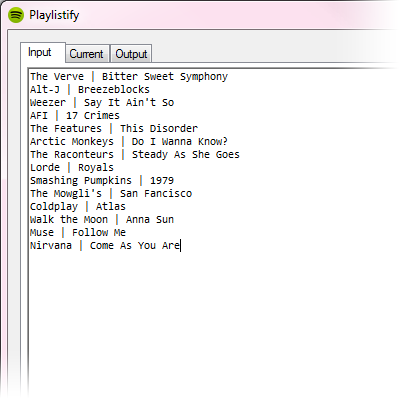
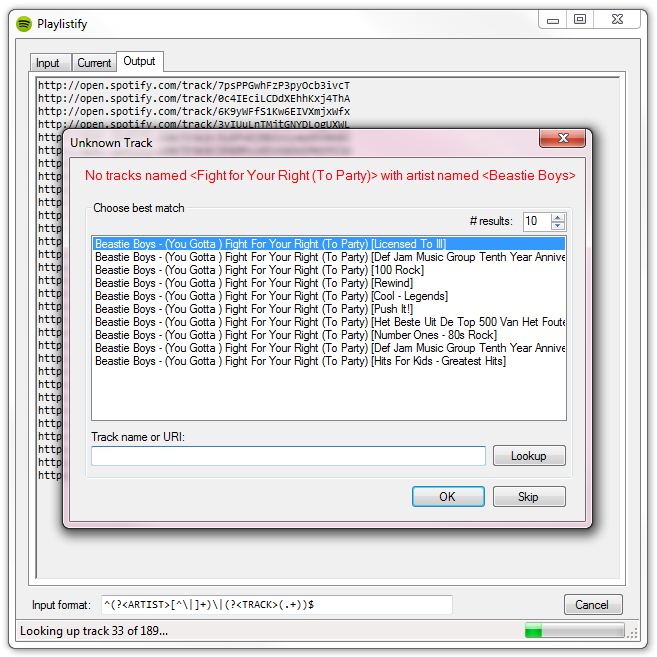
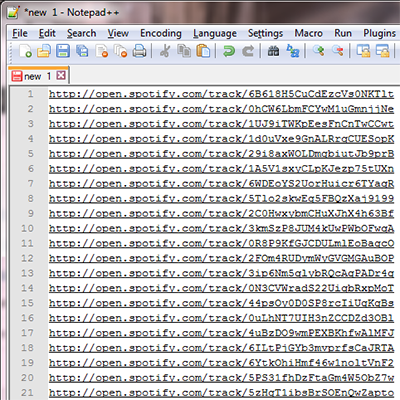
 Sure, right now it looks like crap, but now the data are in a format that can easily be stripped out.
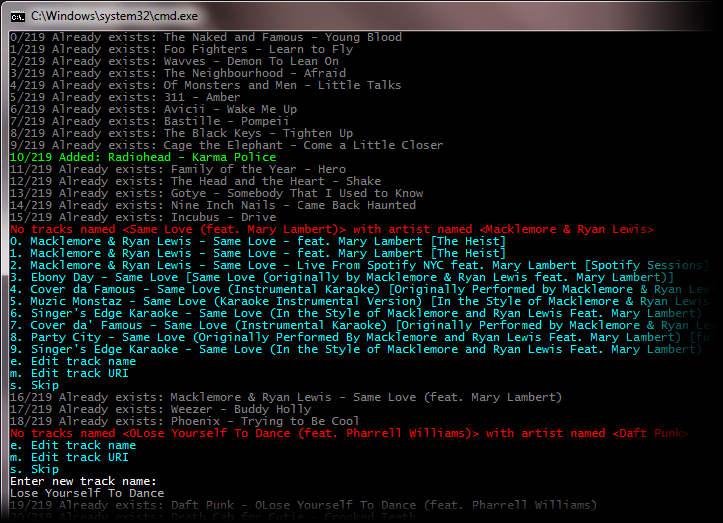
Sure, right now it looks like crap, but now the data are in a format that can easily be stripped out. Voilà! I then copy this list into a text file that will then be read by a command-line tool that hooks into
Voilà! I then copy this list into a text file that will then be read by a command-line tool that hooks into